ilari.scheinin.fi

Ranking NHL’s best shooters – 2018 update

by Ilari Scheinin Posted on April 12, 2018

Last year, I published an analysis that ranks NHL’s best shooters with Bayesian multilevel modeling. Now that the 2017–2018 regular season is over, I have repeated the analysis with an additional year’s worth of statistics (it starts from season 1967–1968). Some highlights are shown below, and the full results table is available here.

I’ll start with a brief recap of the methodology. More details are available in the original blog post.

There are multiple ways to model players’ shooting ability. The simplest is to use the shooting percentage, which is the number of goals scored divided by the number of shots on goal. The metric is simple to define and straightforward to use, but it has two shortcomings.

The first shortcoming is that while it works well for players with a large number shots of goal, there’s more room for random chance for players with few shots. For this reason, the official career shooting percentage leaderboard only includes players with at least 800 shots. What if one wants to evaluate the shot of a young player who has only played for a couple of seasons?

The second point is not as clear of a shortcoming, but many have argued that the gameplay and level of goaltending have changed over the years. As a result, so has the difficulty of scoring goals, and this change is not reflected in shooting percentages of players from different eras.

To take these two issues into account, I have analyzed shooting percentages with Bayesian multilevel modeling. As always with modeling, there are assumptions that are simplifications of reality. The most important one here is the assumption that each player has an innate level of skill, or shooting ability, that does not change throughout their careers. While this is naturally not exactly realistic, it gives us a nice metric that can be used to rank players. And since players’ careers typically span multiple seasons, it also allows us accommodate scoring difficulty not being constant between seasons.

If you’re interesting in more details, please read the original blog post. It also contains full R and Stan code to perform the analysis, and some plots to evaluate its performance.

Results

After updating the model with data from season 2017–2018, here are the overall top 10 shooters. Any changes in ranking from last year are highlighted with arrows and color.

	player	position	career	shots	goals	raw	model
1	Alex Tanguay	forward	1999–2016	1,525	283	18.56%	19.93%
2	Craig Simpson	forward	1985–1995	1,044	247	23.66%	19.85%
3 ↑ 1	Andrew Brunette	forward	1995–2012	1,516	268	17.68%	18.84%
4 ↓ 1	Steven Stamkos	forward	2008–current	2,088	348	16.67%	18.81%
5	Sergei Makarov	forward	1989–1997	610	134	21.97%	18.64%
6	John Bucyk	forward	1967–1978	1,723	329	19.09%	18.38%
7	Mark Parrish	forward	1998–2011	1,247	216	17.32%	18.14%
8	Charlie Simmer	forward	1974–1988	1,531	342	22.34%	18.09%
9 ↑ 48	Patrik Laine	forward	2016–current	445	80	17.98%	18.06%
10 ↑ 7	Paul Byron	forward	2010–current	388	70	18.04%	17.96%

As the most interesting changes from last year are for active players, here is also their top 10.

	player	position	career	shots	goals	raw	model
1	Steven Stamkos	forward	2008–current	2,088	348	16.67%	18.81%
2 ↑ 10	Patrik Laine	forward	2016–current	445	80	17.98%	18.06%
3 ↓ 1	Paul Byron	forward	2010–current	388	70	18.04%	17.96%
4 ↓ 1	Brad Marchand	forward	2009–current	1,426	226	15.85%	17.77%
5 ↓ 1	Adam Henrique	forward	2010–current	1,068	166	15.54%	17.20%
6 ↑ 2	Mark Stone	forward	2012–current	613	95	15.50%	16.55%
7 ↑ 4	Sean Monahan	forward	2013–current	929	138	14.85%	16.42%
8 ↑ 44	Auston Matthews	forward	2016–current	466	74	15.88%	16.42%
9 ↓ 4	Sidney Crosby	forward	2005–current	2,843	411	14.46%	16.30%
10 ↑ 8	Mark Scheifele	forward	2011–current	760	113	14.87%	16.24%

The full results table with 5,573 players is available here.

Posted in R, sports | Comments Off

Ranking NHL’s best shooters with Bayesian multilevel modeling

by Ilari Scheinin Posted on April 17, 2017

Update April 12, 2018: This post is from spring 2017, so the results reflect statistics up to season 2016–2017. I have now re-run the analysis including data from season 2017–2018, and updated results are available here. Methodology is unchanged, so everything below is still an accurate description of how the analysis was performed.

In this post I will look at the question of who have been the best shooters in the NHL. The metric I will use is the shooting percentage, which is the number of goals scored divided by the number of shots on goal. To deal with two issues that will be explained in the next section, I will use a technique called Bayesian multilevel modeling. If that sounds complicated, fear not; it works kind of the same way as human intuition.

After Jake Guentzel scored his first NHL career goal during his first shift in his first game with his first shot, his shooting percentage was 100%. But no reasonable human being would say based on that alone that he was the best shooter of all times with that flawless record. Instead, to evaluate a new player, one tends to start with a vague assumption that their shooting ability is probably somewhat average, but can also be higher or lower. Then, as more and more evidence builds up, that assumption is updated, which leads to a more and more precise picture. This is essentially what “Bayesian modeling” means; start with a prior expectation and update it with the data you have.

There are many ways we can come up with that prior expectation. It could be the average shooting percentage of all players in the league, or defined more narrowly. Depending on the situation, we could for example look only at players who shoot from the right. Or players who are first-round draft picks. Or use the information we have on player position, and assess forwards and defencemen separately. After all, on average forwards do score more goals and in general shoot from much closer to the opponent’s net than defencemen. Here, the use of such a hierarchy, players grouped according to their position, is the “multilevel modeling” part.

When these two are put together, what Bayesian multilevel modeling means for this post is that I will use historical player statistics to estimate average performance separately for forwards and defencemen, and use this average as the starting point to evaluate each individual player. The more evidence there is for any given player, the further away we are ready to move from the average.

This post contains all the code needed to perform the analysis with R and Stan, but the code sections can be freely skipped over if one is not interested in them. Impatient readers can also skip directly to the results section, or just look at the full result table.

Data

Our data consists of the number of goals scored and shots on goal for each player for each regular season. NHL started to count shots on goal for season 1967–1968, so our data spans from that season to the just finished one 2016–2017. Here’s an excerpt of the first ten data rows. 1

	player	position	season	shots	goals
1	Antti Aalto	forward	1997-1998	1	0
2	Antti Aalto	forward	1998-1999	61	3
3	Antti Aalto	forward	1999-2000	102	7
4	Antti Aalto	forward	2000-2001	18	1
5	Spencer Abbott	forward	2013-2014	2	0
6	Spencer Abbott	forward	2016-2017	1	0
7	Justin Abdelkader	forward	2007-2008	6	0
8	Justin Abdelkader	forward	2008-2009	2	0
9	Justin Abdelkader	forward	2009-2010	79	3
10	Justin Abdelkader	forward	2010-2011	129	7

We can aggregate this by player to get raw career shooting percentages.

	player	position	career	shots	goals	raw
1	Antti Aalto	forward	1997–2001	182	11	6.04%
2	Spencer Abbott	forward	2013–	3	0	0.00%
3	Justin Abdelkader	forward	2007–	964	85	8.82%
4	Pontus Aberg	forward	2016–	12	1	8.33%
5	Dennis Abgrall	forward	1975–1976	9	0	0.00%
6	Ramzi Abid	forward	2002–2007	112	14	12.50%
7	Thommy Abrahamsson	defenceman	1980–1981	66	6	9.09%
8	Noel Acciari	forward	2015–	33	0	0.00%
9	Doug Acomb	forward	1969–1970	0	0
10	Keith Acton	forward	1979–1994	1,690	226	13.37%

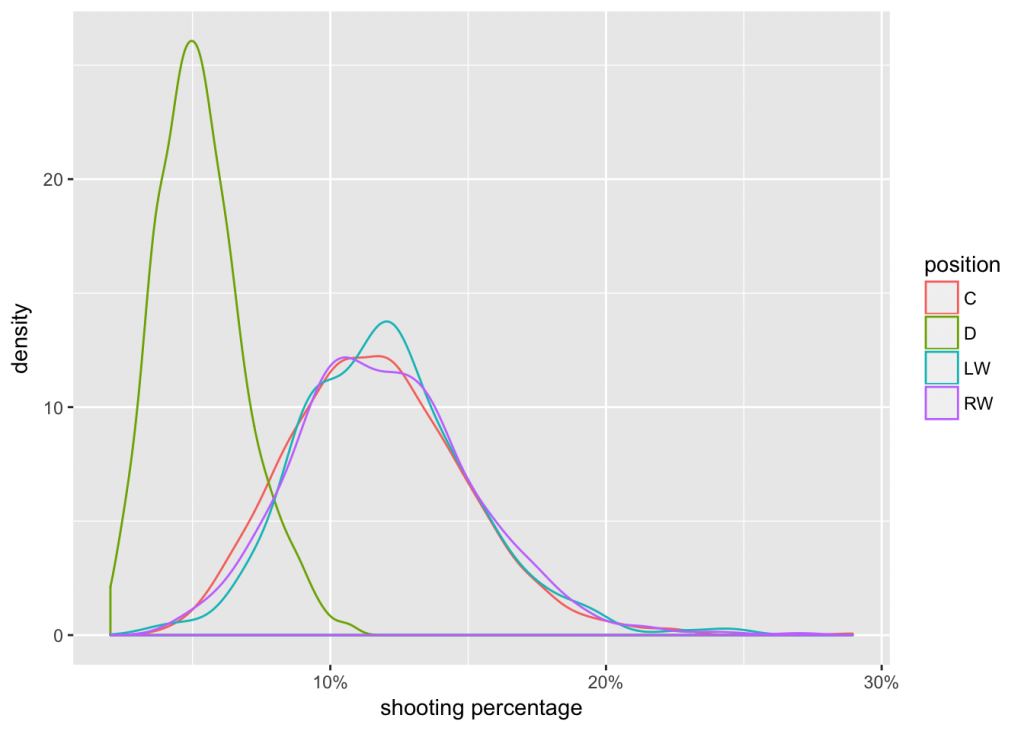
To get an idea of common values for raw career shooting percentage, we make a density plot and separate between forwards and defencemen.

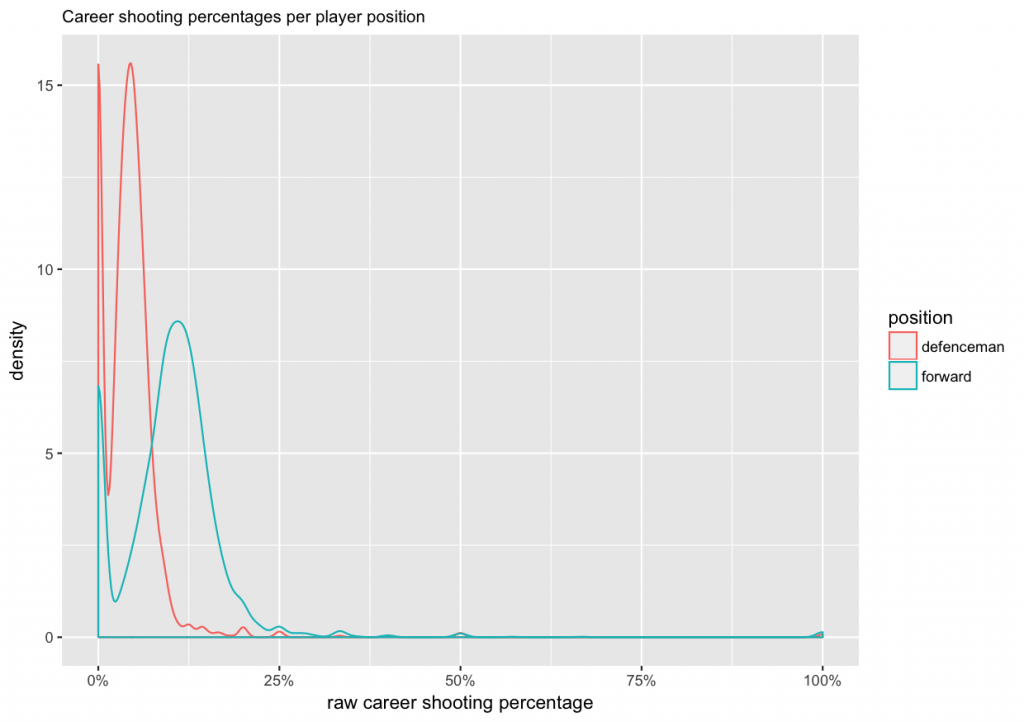
From the plot we can see that:
1. Defencemen tend to have lower shooting percentages than forwards (averages of about 4.5% and 11%).
2. There are big peaks at zero, which represent players who have never scored a goal (and who might also have a very small number of shots on goal).
3. There are also small peaks at 100%, 50%, 33%, etc, which represent players who have a small number of shots on goal, but who got lucky and scored.

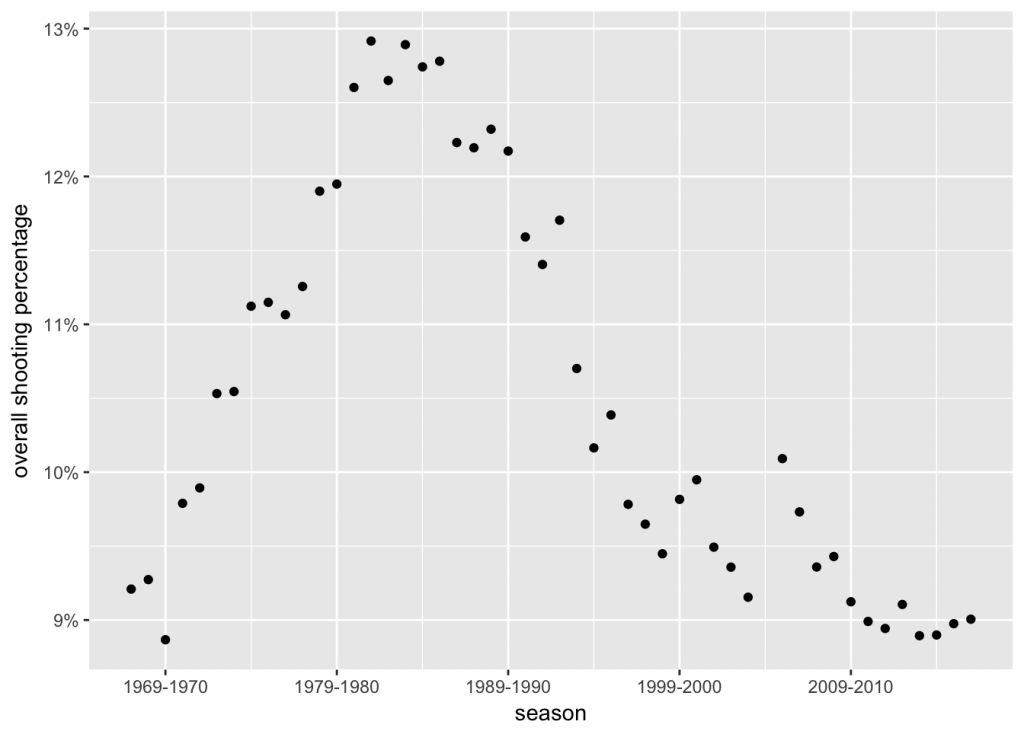
Points 2. and 3. above are the first reason why we use the modeling approach. It will give us with a way to assess players for whom we have little data. The second reason is the fact that the gameplay in the NHL has changed over the years. Nowadays the game is faster, and players have less time and less space to maneuver with the puck and to score. Also, a lot more attention is paid to goaltending, and goalies receive more training and coaching on their technique than in the old days. To assess this change over time, we can plot the overall league shooting percentages per season.

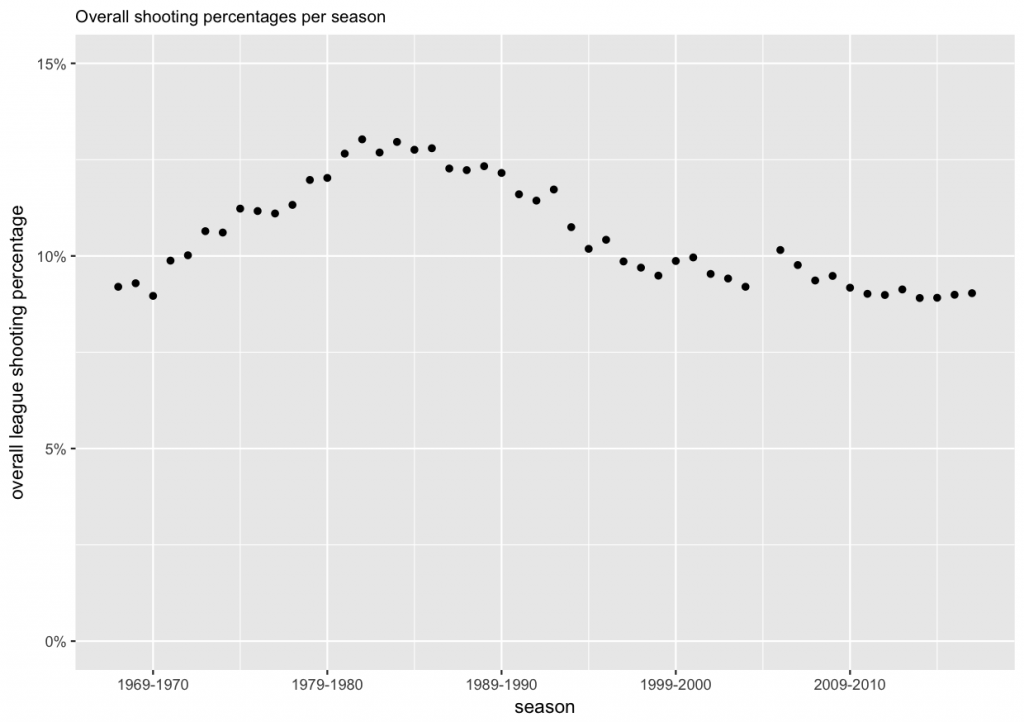
From the plot we can see that the average shooting percentage has indeed changed over time, and was the highest in the 1980s.

Model

For every shot on goal, there are two possible outcomes: a goal or no goal. When we count the number of goals scored (successes) from some number of shots on goal (trials), in statistics this is represented with the binomial distribution. In addition to the number of trials, the number of successes depend on the probability of success for each trial, which here represents the player’s shooting ability, or skill. This probability is assumed to be the same for each trial, which is naturally not really true here. In reality, the probability varies from play to play, and is affected by factors such as distance, proximity of other players, positioning of the goalie, and so forth. But here we make an oversimplification and assume that each player has a constant probability of success that depends on their skill. For any given player on any given season, the number of goals scored is therefore distributed as:

goals scored ~ binomial(shots on goal, skill of player)

Another oversimplification we are going to make is that we assume players’ skills to stay constant not only within a season, but all through their careers. Again, in real life young players develop and get better, and before older players retire, their performance generally shows some decline. But here we are interested in ranking the best shooters, and want to be able to compare players across time, for example current players to those who played in the 1980s. Therefore, we will define the probability of success as the player’s skill minus the difficulty of the season.

goals scored ~ binomial(shots on goal, skill of player – difficulty of season)

The seasonal difficulty represents the combined effect of all other factors besides the player’s skill, such as goaltending, overall gameplay, and so on. We are able to combine these effects, because most players’ careers have spanned multiple seasons. This allows us to fit a model that finds an innate skill for each player (that stays constant throughout their career) and separately captures an estimate for seasonal difficulty.

We fit this model with Stan.

Evaluation

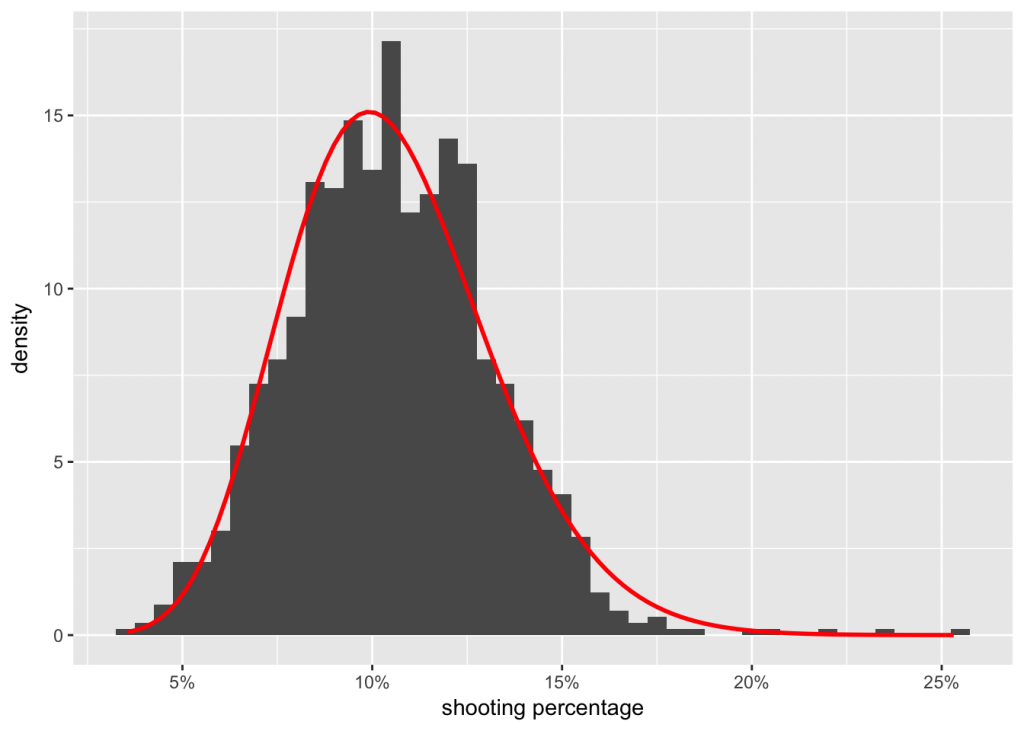
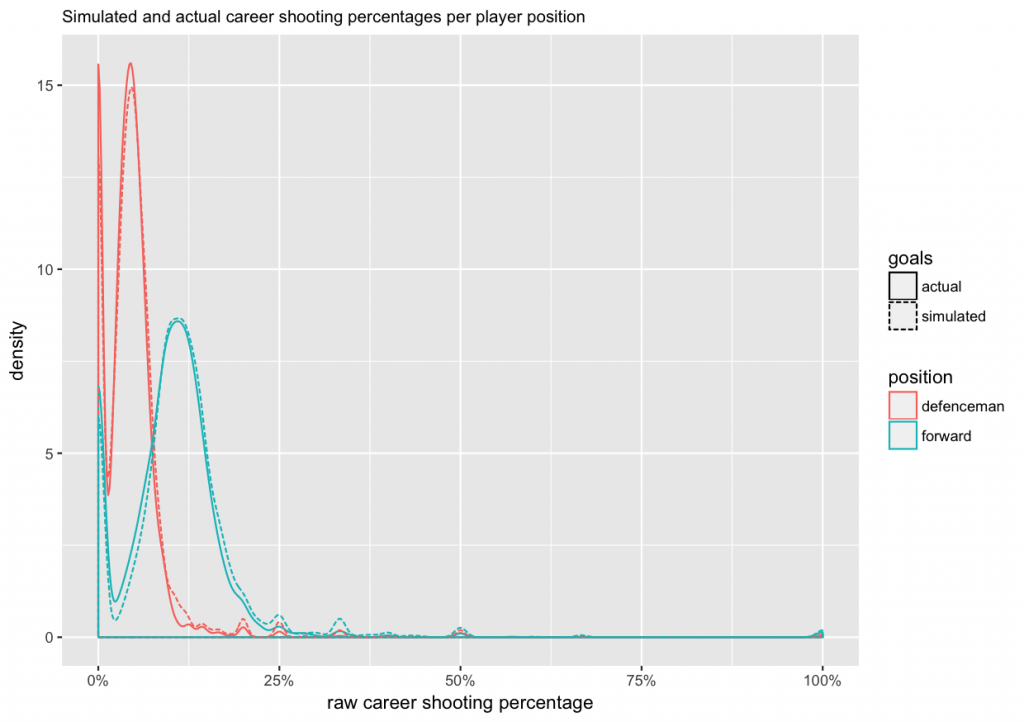
Now that we have fitted our model, we would like to evaluate if it makes sense. One way to approach this is with a simulation. We can use the model (players’ skills, and seasons’ difficulties) and the historical number of shots on goal to generated a simulated set of goals scored. Then we can visualize the actual and simulated numbers, and see if they behave similarly. Let’s start with the same density plot we used above to evaluate typical raw career shooting percentages for forwards and defencemen. Actual results are shown with a solid line, and the simulation results with a dashed line. Ideally, they should be close to each other.

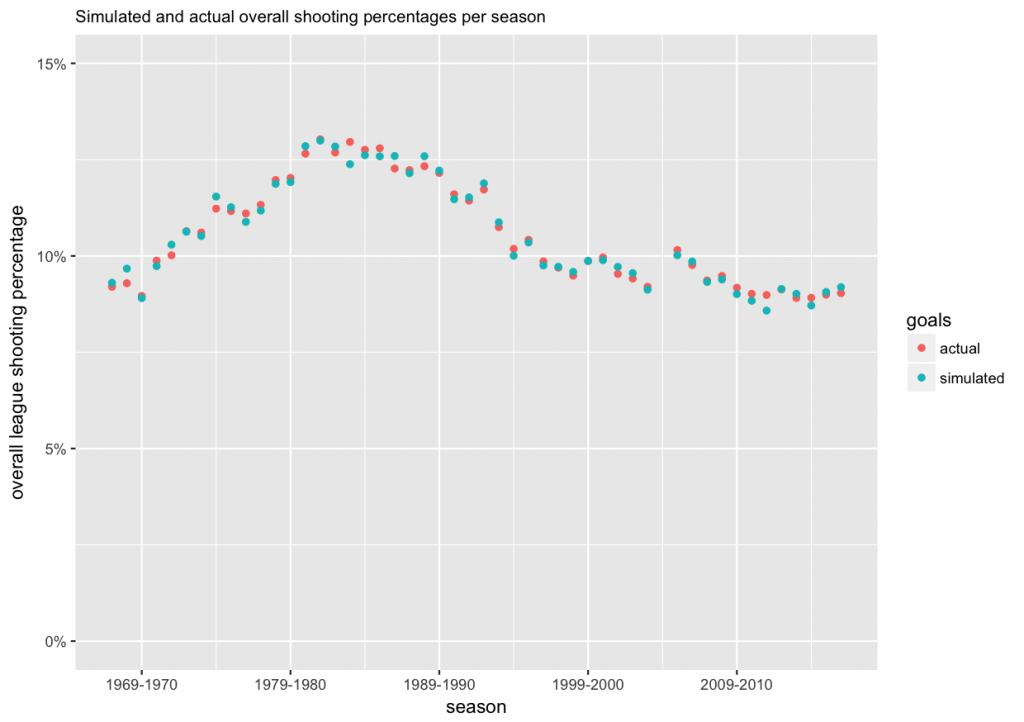
We will also re-create the plot we used above for overall league shooting percentages per season. Again, ideally the actual and simulated data points should be close to each other.

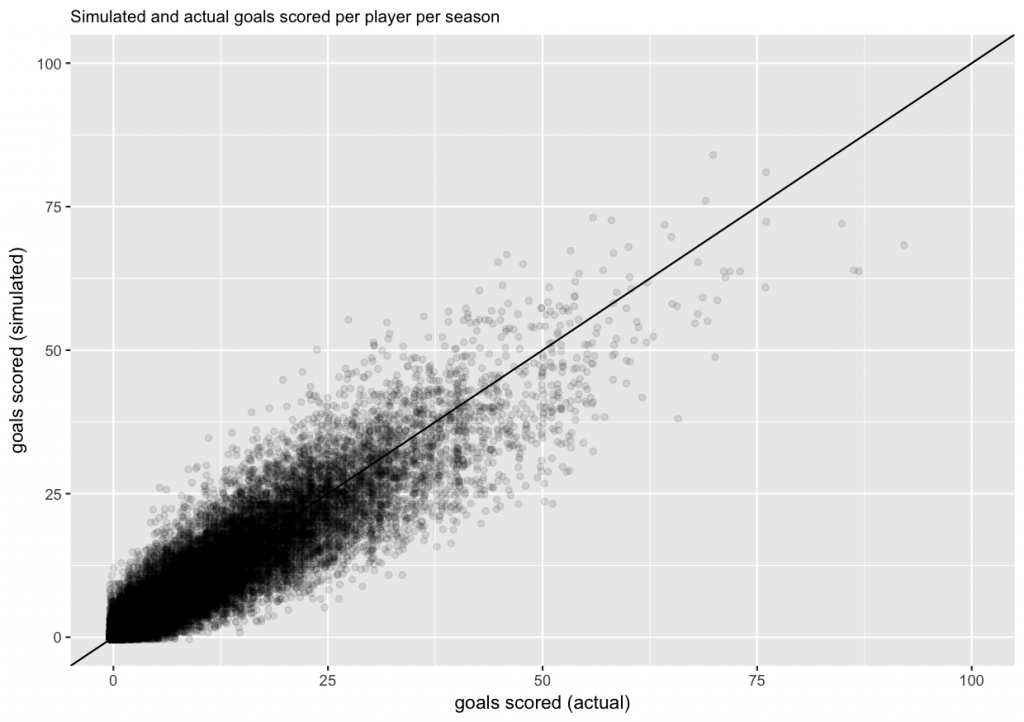
And finally, we will make a scatter plot of actual and simulated goals scored per player per season. Ideally, the cloud of points should be symmetric around the diagonal line.

In the density plot, the fit looks good for defensemen, but for forwards the model seems to slightly overestimate the number of forwards with an average raw shooting percentage (around 11%), and underestimate the number of forwards with low raw shooting percentages. Otherwise the fits seem to be reasonable close. So, let’s look at the results.

Results

When we fit the model, two things happen to the original raw career shooting percentages. First, they are shrunk towards the averages defined separately for forwards or defencemen. Second, they are adjusted for the seasonal difficulty. For players with careers during the “easier” seasons, such as in the 1980s, this will reduce their estimated skill. And for players who played during seasons with a higher estimated difficulty, their skill values will see an increase.

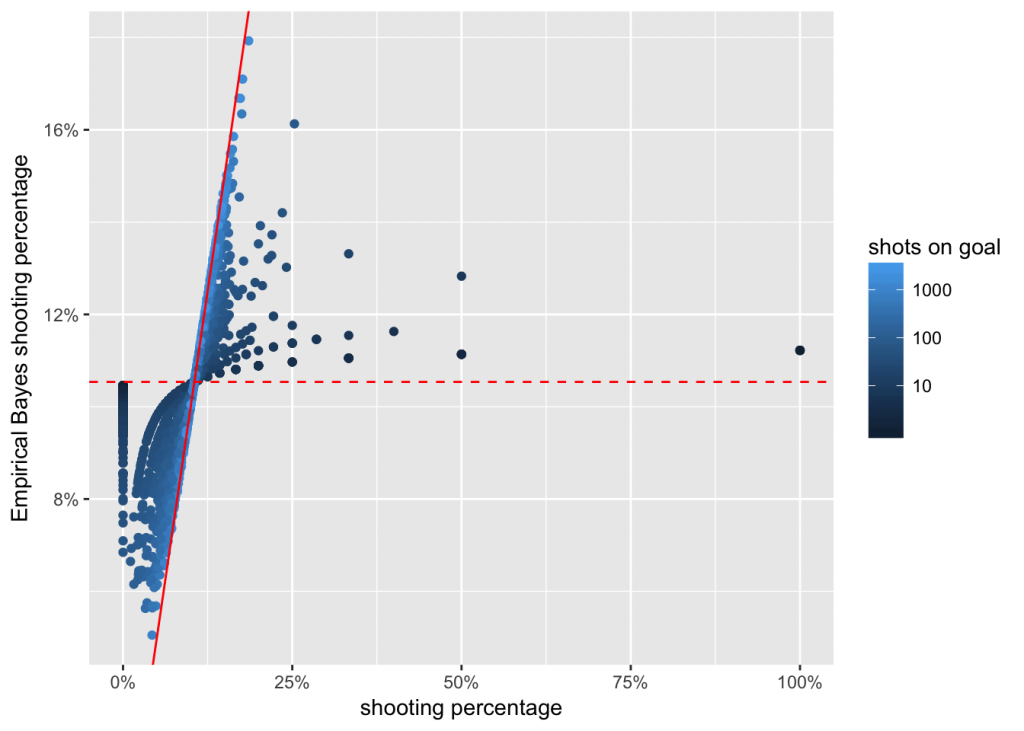
The resulting values, players’ skills, are visualized here together with their raw career shooting percentages.

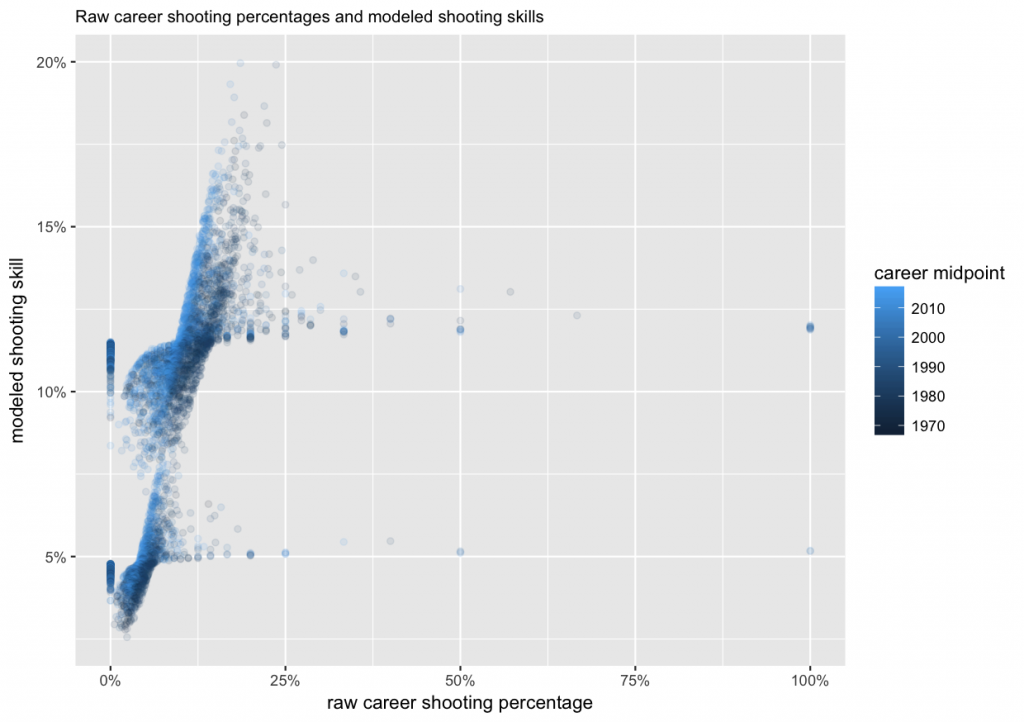
We can see that among the raw shooting percentages on the x-axis, there are extreme values, such as 0%, 100%, 50%, etc. But on the modeled skill on the y-axis, they have been shrunk to all be between about 2% and 20%. Also visible are the two separate clusters for forwards (around 11%–12%), and defencemen (4%–5%). The shades of blue show how the same raw career shooting percentage results in a higher estimated skill for more recent players compared to the 1970s and 80s.

Finally, below are tables of the top 10 forwards and defencemen, ranked according to their modeled shooting skills.

	player	position	career	shots	goals	raw	model
1	Alex Tanguay	forward	1999–2016	1,525	283	18.56%	19.96%
2	Craig Simpson	forward	1985–1995	1,044	247	23.66%	19.91%
3	Steven Stamkos	forward	2008–	1,876	321	17.11%	19.32%
4	Andrew Brunette	forward	1995–2012	1,516	268	17.68%	18.92%
5	Sergei Makarov	forward	1989–1997	610	134	21.97%	18.66%
6	John Bucyk	forward	1967–1978	1,723	329	19.09%	18.39%
7	Mark Parrish	forward	1998–2011	1,247	216	17.32%	18.17%
8	Charlie Simmer	forward	1974–1988	1,531	342	22.34%	18.14%
9	Gary Roberts	forward	1986–2009	2,374	438	18.45%	17.92%
10	Ray Ferraro	forward	1984–2002	2,164	408	18.85%	17.68%

	player	position	career	shots	goals	raw	model
1	Sandis Ozolinsh	defenceman	1992–2008	1,771	167	9.43%	9.55%
2	Shea Weber	defenceman	2005–	2,235	183	8.19%	9.24%
3	Mike Green	defenceman	2005–	1,618	134	8.28%	9.15%
4	Lubomir Visnovsky	defenceman	2000–2015	1,532	128	8.36%	9.00%
5	Bobby Orr	defenceman	1967–1979	2,795	257	9.19%	8.91%
6	Marc-Andre Bergeron	defenceman	2002–2013	951	82	8.62%	8.88%
7	Oliver Ekman-Larsson	defenceman	2010–	1,134	88	7.76%	8.53%
8	Nick Holden	defenceman	2010–	350	32	9.14%	8.45%
9	Tyler Myers	defenceman	2009–	737	59	8.01%	8.45%
10	Mark Giordano	defenceman	2005–	1,295	99	7.64%	8.44%

Craig Simpson holds the official record for best career shooting percentage, which only counts players with at least 800 shots on goal, with 23.66%. But here he has lost the number one spot to Alex Tanguay, who originally ranked 22nd. Their modeled shooting skills are 19.91% vs. 19.96%. This is is due to the fact that Simpson’s career was in 1985–1995, which according to the model was a less difficult era for goal scoring than Tanguay’s 1999–2016.

There are many such differences between the official career shooting percentage ranking and our modeled one. They can be explored from the full table with 5,574 players. It is by no means the right ranking; it is simply a plausible one given the model and assumptions described above. But compared to the official ranking for career shooting percentage, it does have two benefits. First, it does not omit players with less than 800 career shots on goal. And second, it provides one way to gauge changes in gameplay, and thus facilitate comparisons between players whose careers do not overlap. So, while the model’s assumptions are not exactly realistic (an innate shooting skill that stays constant for the duration of a player’s career), the results can be a useful complement to the official career shooting percentage statistics in some situations.

Centers and left/right wingers are all counted simply as “forwards”. This is because multiple players have played both as centers and wingers. The small number who have played both as forwards and defencemen were excluded from the analysis.↩

Posted in R, R-bloggers, sports | Comments Off

Convenient plotting of distribution shapes in R

by Ilari Scheinin Posted on November 18, 2016

I needed to compare the shapes of a few distributions, and therefore wanted an easy way to plot them in R. For example, the standard normal can be plotted quickly enough with curve(dnorm(x, mean=0, sd=1), from=-3, to=3). But when comparing multiple ones, there could be something a bit more handy in terms of keeping track of parameter values for each. So, I ended up writing a little convenience function for that purpose.

As an example, a few beta distributions can be compared with:

plot_dist(dbeta, c(shape1=2, shape2=8))
plot_dist(dbeta, c(shape1=2, shape2=5), col="red", add=TRUE)
plot_dist(dbeta, c(shape1=2, shape2=3), col="blue", add=TRUE)
plot_dist(dbeta, c(shape1=2, shape2=2), col="darkgreen", add=TRUE)

The code for plot_dist() is in this gist.

Posted in R | Comments Off

How good is Patrik Laine’s shot?

by Ilari Scheinin Posted on November 16, 2016

Patrik Laine is playing his first season in the NHL and currently leads the league in scoring with 12 goals. With 51 shots on goal, his shooting percentage is 23.5 %. How does this number compare to great goal scores over the years? I downloaded NHL player statistics for each season from 1967–1968 onwards, which was the first year the number of shots was recorded. I then calculated career summaries for each player. But if we simply look for players with the highest shooting percentages, the first 12 all scored one goal with just one shot. Obviously these are not the best shooters, just some random flukes. In its official leaderboard for all-time career shooting percentage (S%), the NHL only counts players with at least 800 shots. This is what the top 10 looks like:

	Name	Pos	GP	G	A	PTS	S	S%
1	Craig Simpson	LW	634	247	250	497	1,044	23.7
2	Charlie Simmer	LW	712	342	369	711	1,531	22.3
3	Paul MacLean	RW	719	324	349	673	1,513	21.4
4	Mike Bossy	RW	752	573	553	1,126	2,705	21.2
5	Yvon Lambert	LW	683	206	273	479	1,038	19.8
6	Rick Middleton	RW	1,005	448	540	988	2,275	19.7
7	Blaine Stoughton	RW	526	258	191	449	1,322	19.5
8	Darryl Sutter	LW	406	161	118	279	829	19.4
9	Rob Brown	RW	543	190	248	438	979	19.4
10	Mike Ridley	C	866	292	466	758	1,513	19.3

Requiring a minimum number of shots (or goals) does get rid of the flukes, but how can you compare a rookie player? What kind of method could be used to take the scarcity of evidence into account, until the player catches up with the threshold? David Robinson has written a terrific series of articles for situations like this, using baseball statistics as an example. I’ll follow one of his tutorials and use empirical Bayes estimation to obtain a more reliable picture. In short, we’ll first use all players’ data to obtain an estimate for a beta prior, and then use each player’s own data to update the prior based on individual evidence. Put another way, we start by assuming everyone is average, and if and only if they show more and more evidence to the contrary, we start to gradually consider them as special. For a more much better description, please see the original blog post. All R code is also adapted from that post.

Before we get to estimation of the beta prior, let’s first check if we should use all of the available data or only a subset. Since in this case we are estimating only one prior, we would like all players to come from a single distribution. As the gameplay has surely changed a bit over the years, let’s look at the overall shooting percentages over the 49 seasons. Also, since defensemen normally play futher away from the opponent’s net than forwards, player position is likely to have an effect as well. Let’s look at shooting percentages separately for each position (excluding players with less than ten goals).

As we can see, shooting percentages used to be much higher around the 1980s. For this simple analysis, I’ll only include data from season 1996–1997 onwards. I’ll also leave out the defensemen, as they tend to have lower shooting percentages. (I hope to write follow-ups posts later with all of the data included and handled properly, either using some of the other approaches David has described for empirical Bayes, with a standard Bayesian analysis, or maybe even both.)

Overall, the average shooting percentage for all forwards over the last 20 seasons is 11.0 %. Next, let’s estimate a beta prior from the data and see how it fits:

Shooting percentages can now be adjusted using this prior. This will shrink individual players’ estimates towards the horizontal dashed line. The more evidence there is for an individual (the brighter the blue dot), the more we trust it. The darker dots show a lot of shrinkage, whereas the light ones are much closer to the diagonal red line, which marks the case of no shrinkage at all.

Finally, let’s look at the ranking (from season 1996–1997 onwards) for shooting percentage estimated with empirical Bayes (EB). Patrik Laine currently sits at number 40, and only time will tell where he moves on that list. But what we do know today, is that he is one of only four 18-year-olds to score two hat tricks in the NHL (others being Jack Hamilton, Dale Hawerchuk, and Trevor Linden), and he still has the rest of the regular season to hunt for a third one before his 19th birthday on April 19th, 2017.

	Name	Pos	GP	G	A	PTS	S	S%	EB
1	Alex Tanguay	LW	1,088	283	580	863	1,525	18.6	17.9
2	Andrew Brunette	LW	1,099	265	462	727	1,500	17.7	17.1
3	Steven Stamkos	C	586	321	261	582	1,876	17.1	16.7
4	Mark Parrish	RW	722	216	171	387	1,247	17.3	16.7
5	Dmitri Khristich	C	420	111	171	282	633	17.5	16.3
6	Mike Ridley	C	75	20	32	52	79	25.3	16.1
7	Tomas Holmstrom	LW	1,026	243	287	530	1,489	16.3	15.9
8	Gary Roberts	LW	639	181	224	405	1,120	16.2	15.6
9	Brenden Morrow	LW	991	265	310	575	1,670	15.9	15.5
10	Jan Hrdina	C	513	101	196	297	619	16.3	15.3
11	Jason Allison	C	519	152	326	478	962	15.8	15.2
12	Ziggy Palffy	RW	565	276	333	609	1,799	15.3	15.0
13	John LeClair	LW	624	281	274	555	1,833	15.3	15.0
14	Alexander Mogilny	RW	530	207	274	481	1,341	15.4	15.0
15	Pierre Turgeon	C	622	197	351	548	1,285	15.3	14.9
16	Tyler Bozak	C	451	112	169	281	717	15.6	14.8
17	Sergei Kostitsyn	LW	353	67	109	176	414	16.2	14.8
18	Joe Nieuwendyk	C	628	236	242	478	1,555	15.2	14.8
19	Anson Carter	RW	674	202	219	421	1,331	15.2	14.8
20	Tony Hrkac	C	425	70	105	175	438	16.0	14.7
21	Mark Messier	C	555	155	264	419	1,015	15.3	14.7
22	Yanic Perreault	C	742	217	237	454	1,436	15.1	14.7
23	Adam Deadmarsh	RW	441	154	154	308	1,010	15.2	14.7
24	Adam Henrique	C	364	101	109	210	650	15.5	14.7
25	Teemu Selanne	RW	1,192	521	594	1,115	3,528	14.8	14.6
26	Jonathan Toews	C	662	255	321	576	1,710	14.9	14.6
27	Jiri Hudler	C	680	161	256	417	1,068	15.1	14.6
28	Paul Byron	C	217	34	43	77	198	17.2	14.5
29	Brad Marchand	C	470	158	147	305	1,057	14.9	14.5
30	Sidney Crosby	C	716	348	603	951	2,376	14.6	14.4
31	Mike Sillinger	C	831	210	234	444	1,420	14.8	14.4
32	Keith Tkachuk	LW	893	394	382	776	2,713	14.5	14.3
33	Peter Forsberg	C	579	204	515	719	1,390	14.7	14.3
34	Milan Lucic	LW	664	164	242	406	1,111	14.8	14.3
35	Dany Heatley	RW	869	372	419	791	2,565	14.5	14.3
36	David Desharnais	C	420	78	168	246	511	15.3	14.3
37	Martin Straka	LW	714	206	370	576	1,408	14.6	14.3
38	Thomas Vanek	LW	824	320	337	657	2,213	14.5	14.2
39	Stephane Matteau	LW	471	75	88	163	493	15.2	14.2
40	Patrik Laine	RW	18	12	5	17	51	23.5	14.2

Posted in R, sports | Comments Off

Boat trips and weather observations

by Ilari Scheinin Posted on October 20, 2016

Another boating season is over, so I updated the shiny app of my boat trips with another year’s worth of Moves app data.

I also added weather and wave observations from the API of the Finnish Meteorological Institute. Clicking on a track brings up these details, provided the closest weather stations and wave buoys are within 30 nautical miles from the track. They are therefore only approximations, and can vary from the conditions actually experienced on the boat, depending on its location relative to the stations/buoys and nearby islands.

It should also be noted that the tracking accuracy of Moves is lower than that of proper chart plotters, which is only natural considering battery consumption. There are also clear errors when close to shore, as Moves has a tendency to place the location on known roads. Tracks and all values should therefore be taken with a grain of salt.

The source code can be found on GitHub, and the app itself is here.

Posted in R, sailing, transportation | Comments Off

Finland’s dependency ratio and pension contributions

by Ilari Scheinin Posted on October 20, 2016

In March, I made simple visualizations of Finland’s population structure and statutory pension contributions. I also made a third one, combining the two topics, but never posted it. Here it is.

Shown in white is the aged dependency ratio, which is the proportion of people aged 65 and over, compared to those between 15 and 64. A solid line shows historical data, and future predictions are shown with a dashed one. The blue line shows statutory pension contributions as percent of GDP.

I agree with the former MP Kimmo Kiljunen in that the capital amassed in pension funds should be used. But I disagree with him when he says that they should be used to increase pensions. Instead, they should be used to keep pension contributions from skyrocketing along with the dependency ratio.

That’s the very reason why these funds were accumulated in the first place.

The code to generate the figure above is in this gist.

Posted in R | Comments Off

Finland’s mandatory pension contributions

by Ilari Scheinin Posted on March 9, 2016

A couple of weeks ago, I made an animated visualization of the population structure of Finland. Here’s another plot exploring demographic changes, this time coupled with the economy.

Finland has a defined-benefit and earnings-related statutory pension system. Employers are required by law to pay pension contributions of 24.0 % on top of an employee’s gross salary. In addition, the employee is required to pay a contribution of 5.7 %, or if they are 53 years or older, 7.2 %. These contributions are used to pay out the current pension liabilities. (The system is partly funded, but currently more is paid out than collected.)

Here’s a plot of the total contributions as a percentage of the gross domestic product (GDP).

The R code to produce the plot is in this gist.

Posted in R | Comments Off

Population Structure of Finland

by Ilari Scheinin Posted on February 27, 2016

Inspired by the blog post Japan’s aging population, animated with R by David Smith and the population pyramid plot by Kyle Walker, I figured I’d try the same for Finland.

I used the pxweb package (by Måns Magnusson, Love Hansson, and Leo Lahti) to pull the corresponding data from Statistics Finland, and plotted it by making some adjustments to Kyle’s code.

The R code to generate the animation is in this gist.

Posted in R | Comments Off

Snowplows of Helsinki

by Ilari Scheinin Posted on February 7, 2016

As part of the Helsinki Region Infoshare initiative, the city of Helsinki provides an API that shows the locations, routes, and activities of snowplows that are operated by its service provider Stara.

Using that API, Sampsa Kuronen created Aurat kartalla, which is a beautiful visualization of the real-time data. It allows you to specify a time interval, and shows different activities (snow removal, spreading sand, de-icing with salt, etc) with different colors.

I decided to try my own version with shiny, for a couple of reasons:

In addition to identifying different activities, the API also includes a flag specifying “bicycle and pedestrian lanes”. Aurat kartalla always shows them with the same color, therefore not distinguishing between e.g. spreading sand and de-icing with salt. Although I personally don’t really mind that much, for some cyclists this is important information. Many have suffered flat tires because of the sand, and many feel that the salt rusts their bikes.
Outside bicycle and pedestrian lanes, Aurat kartalla does show the different activities with different colors. But when there are multiple activities performed on the same route, it can be difficult to tell them apart.
I had never created a shiny app that polls an external API and automatically updates its data, so it was simply an interesting experiment.

Here are links to the resulting shiny app and its source code on GitHub.

As my goal was to provide granular control to really check what activities had been performed along a specific route, at first I included a separate setting to distinguish between streets and bicycle/pedestrian lanes. However, after looking at the results on a couple of snowy days, I noticed that this flag wasn’t really that reliable. Exact same routes were plowed both with and without it.

I can think of two possible explanations. The first one is that the flag really just specifies the equipment used, and some plows are marked for bicycle/pedestrian lanes, while others are not. And that in reality, both can also operate outside these target routes. The second one is that the presence of the flag relies on the plow driver explicitly specifying when they are plowing a bicycle/pedestrian lane, and that this is simply often forgotten (as, to be honest, I would expect to happen in reality).

Therefore, I removed the separation between streets and bicycle/pedestrian lanes, and instead show both at the same time. But the main point is still to be able to unambiguously distinguish between the different activities that have been performed. However, this goal suffers a bit from the fact that the API doesn’t actually contain all of the plows in use, so there is no way to tell for sure whether something has not been performed.

Nevertheless, it was a fun experiment. And in any case, I think Aurat kartalla provides a more beautiful overall visualization of the same data, and with better performance.

Posted in R, transportation, urban | Comments Off

Mapping my boat trips

by Ilari Scheinin Posted on January 31, 2016

Now, in the middle of winter and when I’m a feeling bit under the weather, it’s a perfect moment to reminisce about summer and time spent on the Finnish Archipelago Sea. So, I combined tracking data from the Moves app with some shiny and leaflet code to make an interactive map that shows my boat trips from the last two years.

The source code can be found on GitHub, and the app itself is here.

Zooming in on the tracks brings back memories from all those legs and marinas, of great sailing and even better company. It lets me relive moments like these.

Posted in R, sailing | Comments Off